QA Innovative Solutions

In Performance testing, a workload model (also known as WLM) is method to represent the expected user behavior, user concurrency on system under test. It helps to simulate the real-world conditions in your scenarios and execute tests to measure the performance of your system. A workload refers to the distribution of load across the identified test scenario.

Before running a performance test, a pattern to be prepared to simulate the production workload, set up the test environment and tools, and establish a baseline for your tests, and so on.

A performance test engineer defines the workload model to simulate the real-world situation in the performance test environment. In the performance test execution cycle, different workloads are prepared to analyze the behaviour of the system under different loads and conditions.

An inaccurate workload pattern can misguide the optimization efforts for tuning the system, delayed application deployment in production, lead to failures, and an inability to meet service-level agreements (SLA) for the system. Designing the right workload model is very crucial for the reliable & robust deployment of any application intended to support a huge volume of concurrent user loads in a production environment.

How to design a workload model accurately

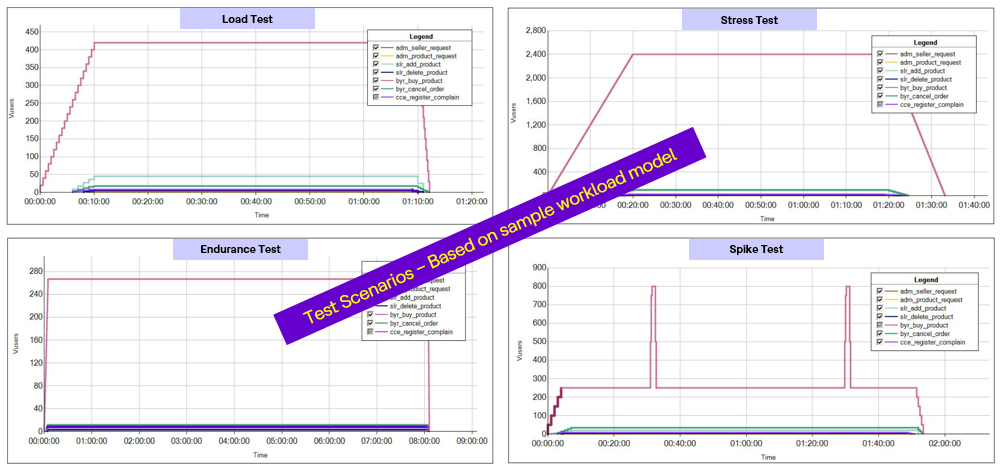
First, you need to identify how many different types of tests scenarios are to be executed as per Performance Test Plan. Each Load, Stress, Volume and Endurance test will have a separate workload model. For example, the users count in the load test will be less in compared to stress test. Hence, both will have separate workload models.

Now, you need collect the respective metrics for all the identified scenarios. Below is the list of metrics to design a workload model accurately:

• Number of User loads
• Test (Iteration) duration
• End-to-End Response Time (Iteration Response Time)
• Number of Transactions
• Pacing and Think Time
• Hits (Requests) per second (TPS)
• Throughput
• Individual page response time

Some of sample test scenarios are given based on sample workload patterns as below:

Maximum Running Users	2000
Ramp up	2 user every 5 seconds
Ramp down	5 users every 7 seconds
Duration of Run at Peak Load	1 hour
Transaction per Second (TPS)	300

Little’s Law Concept in Workload Model Design

Little’s law can be considered as one of the most famous queuing theories. In 1954, a professor “John Dutton Conant Little” at the Massachusetts Institute of Technology published a paper in which he described the queueing theory by a new law. Later on, it was named Little’s Law. John Little formulated 3 basic terms: the average number of customers, customer arrival rate and the average time spent by a customer in the system.

Little’s Law Statement: The long-term average number L of customers in any queueing system is equal to the long-term average effective arrival rate λ multiplied by the average time W that a customer spends in the system. Expressed algebraically the law is:

L = λ * W

The same law is applied in performance testing also and simulate the real-world load on the system under test. So, Little’s law can be rephrased as – A average number of users (N) active in a queuing system is equal to the average throughput (rate of transactions) of system X, multiplied by the average response time (R) of system.

Numerically,

N = R * X

Where,

N = average number of users in a system

X = average throughput or departure rate of users

R = average time spent in the system or response time

Modifying above stated law for performance engineering and adding think time (TT)

N = (R + TT)* X

Calculate Concurrent User loads in a performance test based on following data –

Scenario 1: A system is required to process 2400 transactions/hour with an average response time of 5 seconds per transaction. The average Think Time per user is = 10 seconds. How to find out the concurrent users on the system?

Throughput or X = 2400/3600 = 0.66 TPS (Transactions Per Second)

From Littles Law : N = [R + TT] * X

Applying the equation: N = [ 5 + 10 ] * 0.66 = 10

We can say that now, System is required to have approx. 10 concurrent users to process 2400 transactions per hour.

Scenario 2: For example, while looking at Google Analytics for a given average day, during a peak hour we had:

• 2000 visitors in 60 minutes
• 10,000 page views
• avg page views 5
• avg time on website 7 minutes

So, we want to figure out how many concurrent users should feed into LoadRunner/Jmeter tool to simulate this traffic as a baseline.

So, we need to run approximately 233 concurrent users to maintain the peak load in the system.

Scenario 3: Calculate the concurrent users using Little’s Law. Let’s say that we have set pacing to 15 sec and Think Time to zero.

A vuser performs 5 transactions and response time for each transaction is 10 seconds. But the fact that now pacing is greater than response times, it will override the response times and it will control the transaction rate.  Thence it will take 5*15 = 75 seconds to complete 5 iterations.  i.e. 5/75 = 0.067 TPS

This is the most correct way of setting up your test scenario to simulate consistent TPS load on the system under test.

In the second example, as long as the average response times are less than 15 seconds, it will always take 75 seconds to complete 5 iterations i.e. generate 0.067 TPS

In the above examples, we also assumed that think time was set to Zero. If, say, it was 2 seconds, total time taken to complete 5 transactions would still be 5*15 = 75 seconds i.e. generate (5/75) = 0.067 TPS

Once you understand this concept, rest understanding of Little’s law is easy.

If pacing is set to zero, then

Number of Vusers = TPS * (Response Time + Think Time)

If pacing is ≠ zero and pacing > (response time + Think Time) , then the above formula would look like this

Number of Vusers = TPS * (Pacing)

The fact that TPS is a rate of transactions w.r.to time, it is also called as throughput.

So Little’s law is:

Average number of users in the system = average response time * throughput

N =  ( R + Z )  *  X

Where, N = Number of users

R = average response time (now you know, it can be pacing too)

Z = Think Time

X = Throughput (i.e. TPS)

Example, If N = 100, R = 2 sec, 100= (2+Z)*X and hence –> If Z=18, X = 5